leetcode 137. 出现一次的数字Ⅱ

预览

题目大意

  题目意思很简单，就是找出哪个出现三次的数字，就地运算还要求线性时间复杂度，就是只遍历一次，且不创建其它数据结构。

分析

  这个问题不太好思考，先看一个比较简单的版本。

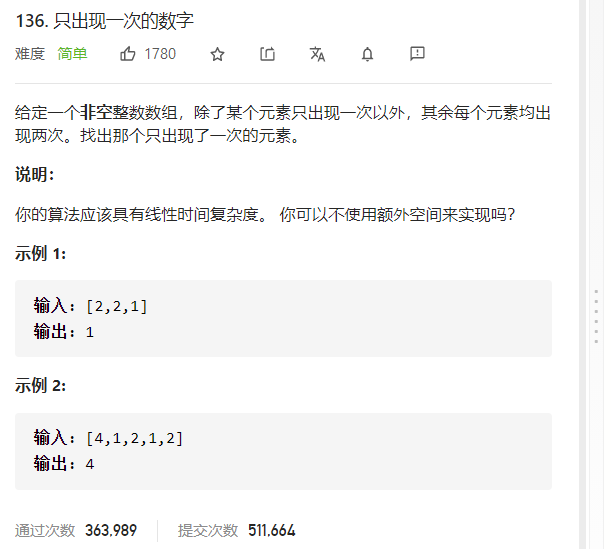
这个问题相对简单，只是其它数字出现的次数从3变成了2，熟悉位运算的人可能就知道两个相同的数异或后为0，且0与一个数异或的结果是 它本身。因此这道题可用异或运算将其解出。

lc136代码

    int singleNumber(vector<int>& nums) {
        int ret = 0;
        for (int n : nums) {
            ret ^= n;
        }
        return ret;
    }

lc137解决

这个问题还是上一个题的延申，还是可用异或去解决。上一个问题是使相同的数异或后变成了0，然后再异或哪个只出现一次的数字就得到了结果。 如果我能让出现三次的数通过某种运算后也让它变为0，那么这个问题就解决了。但是单纯的异或运算并不能达到这个目的。 这里需要修改一下。首先需要两个开关 once, twice,它们分别代表出现一次的数字和出现两次的数字。 可以知道，出现两次的数字要在出现一次的基础上继续迭代。而且当数字出现三次时，此时once，twice都要归零，这样才能保证最后的结果是出现一次的哪一个数字。

lc137代码

    int singleNumber(vector<int>& nums) {
        int once = 0, twice = 0;
        for (int n : nums) { 
            once = (~ twice) & (once ^ n); 
            twice = (~ once) & (twice ^ n); 
        }
        return once;
    }

结合代码来看，如数字序列为：a,a,a,b。初始化时once，twice都为0。当twice为0的时候，这时候once是a， 此时twice ^ n 和once是一样的数字a，再 & (~ once)结果就变成了0,此时第一轮迭代结束。再看第二轮，这时候once ^ a = 0(once在上一轮的结果是a)， 这时候注意看twice， once=0相当于把左边这个开关完全打开了，然后twice ^ a = a,因此最终结果也是a，代表a出现了两次。再看第三轮迭代，此时，once 由于twice开关的存在又会变为0， twice会因为相同的数字异或也变成了0，此时第四轮迭代，once就变成了b。

总结

   位运算确实看起来比较优雅简洁，但是不太好想。