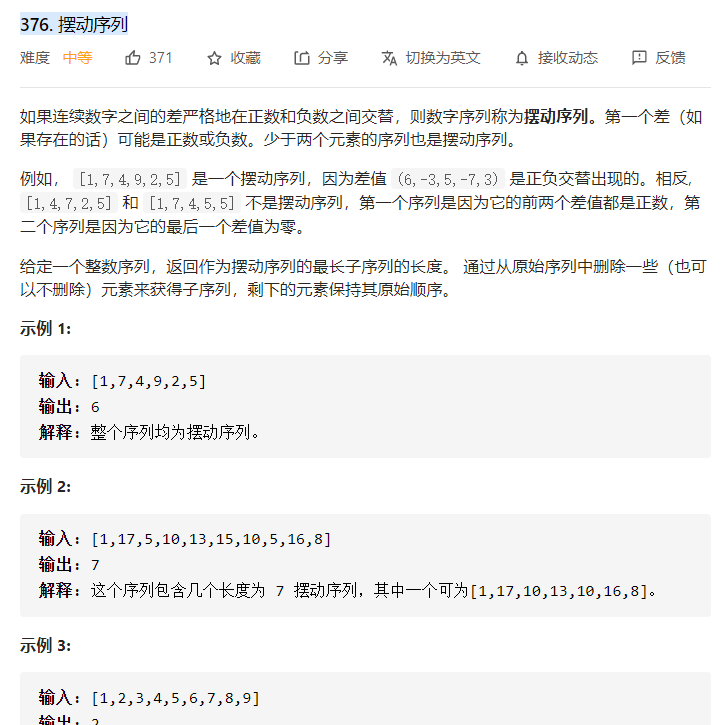
# 题目
# 分析
这个题目的意思就是给定一个整数序列,要求找出作为摆动序列的最长子序列长度。所谓摆动序列是指序列中相邻元素的差值严格按照正负交替组成的序列。
严格暴力肯定可以的,那时间复杂度太高了,然后我一开始的想法是参照最长上升子序列的思想,用二重循环的动态规划去做,因为最长上升子序列的思想很简单,就是一重循环遍历每个元素,二重循环,从最初的元素到达当前元素,并判断是否以当前元素结尾能构成最长上升序列并记录最大长度。迁移到本题上来的话,就需要多一个 flag 标记每个元素之前是上升还是下降,上升的话下一个就找比他小的元素,下降的话就找比他大的元素。代码如下:这个代码写得不好,还写了很久,主要是初始化和第一个元素选择哪里改了一下。
初始化需要明确变量的初值,我这里定义了 flag[i] =0 升,1 降,-1 相等,第一个元素的 flag 标记不重要,由于我从第二个元素开始遍历并且会根据与第一个元素的大小关系改变其 flag[i]标记,所以这里 flag 数组初始化为-1。
遍历到每个元素的时候,判断其与第一个元素的关系的时候不需要判断其 flag[i],因为两个元素只要不相等都可以构成摆动序列。
# dp(O(n^2))代码
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return n;
}
vector<int>dp(n,1);
vector<int>flag(n,-1);//0升,1降,-1差值为0
int ret = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if(j == 0 && nums[i] != nums[j]) { // j == 0 的时候只需要保证 nums[i] != nums[j]即可保证他们两个组成的序列一定是摆动序列
dp[i] = 2;
if (nums[i] > nums[j]) {
flag[i] = 0;
} else if (nums[i] < nums[j]) {
flag[i] = 1;
}
} else if((flag[j] && nums[i] > nums[j])){
if (dp[i] < dp[j] +1) {
dp[i] = dp[j] + 1;
flag[i] = 0;
}
} else if((! flag[j] && nums[i] < nums[j])){
if (dp[i] < dp[j] +1) {
dp[i] = dp[j] + 1;
flag[i] = 1;
}
} else{ // nums[i] == nums[j]
if (dp[i] < dp[j]) {
dp[i] = dp[j];
flag[i] = flag[j];
}
}
ret = max(ret, dp[i]);
}
}
return ret;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
上面的代码真的是又臭又长时间复杂度又高!....
# dp(o(n))
看了官方题解才知道可以用 o(n)的 dp 解决,大概思想是将序列拆分成上升序列和下降序列,这里的上升序列和下降序列是指序列的最后的趋势是上升还是下降决定的。因此,需要构造两个数组,up[],down[],up[i]表示前 i 个元素中最后上升摆动序列的最大长度,同理,down[i]表示前 i 个元素中最后下降摆动序列的长度。这里就要构造状态转移方程了。
初步想法是
up[i] = max(up[i-1],down[i-1]+1) (...能够构成最终上升序列条件)
down[i] = max(down[i-1],up[i-1]+1) (...能够构成最终下降序列条件)
但问题就是后续的条件不好判断,后面这个条件是为了使最后一个数构成对应序列。前面 o(n^2)的 dp 是挨个挨个判断,那这里要降到 o(n)就不能这样了。这里参见官方题解的证明。
以 up[i]为例,通过和前一个元素作比较,即 nums[i]与 nums[i-1],因为这里要找最后是上升的摆动序列,说明之前最后一段是下降趋势。
- 当 nums[i]>nums[i-1]的时候,一定可以找到之前的一个波谷(就是离当前元素最近的下降的哪一个),在这个波谷的基础上再加上当前元素构成的序列一定是最终是上升的摆动序列。这里必须要说明为什么最后一个数能够构成最终是上升的摆动序列
- 当第 i-1 个元素(前一个元素)是波谷的时候,这时候由于 nums[i]>nums[i-1],一定可以加在后面构成摆动序列
- 当波谷是第 i-1 个元素之前的元素时,如果这个元素比第 i-1 个元素大,那么可以通过画图知道,这时候波谷一样可以替换成第 i-1 个元素,整个序列的长度不会改变,然后这时候又可以归到上一类了。
- 当波谷是第 i-1 个元素之前的元素时,如果这个元素比第 i-1 个元素小或者等于,那么肯定这个波谷也比当前第 i 个元素小,那么可以加在后面。
- 当 nums[i] < nums[i-1]时,这时候当前元素不必加入序列。原因如下:
- 当第 i-1 个元素(前一个元素)是波谷的时候,这时候由于 nums[i]<nums[i-1],这时候不可能加上去。
- 当波谷是第 i-1 个元素之前的元素时,如果这个元素比第 i-1 个元素大或者等于,那么更不可能加上去了。
- 当波谷是第 i-1 个元素之前的元素时,如果这个元素比第 i-1 个元素小并且比第 i 个元素大,还是加不了。
- 当波谷是第 i-1 个元素之前的元素时,如果这个元素比第 i 个元素小,这时候第 i-1 个元素和第 i 个元素都可作为最终是上升的摆动序列的最后一个,所以 up[i]与 up[i-1]值相同,直接用 up[i] = up[i-1]就好了。
当 nums[i] == nums[i-1]时,跟小于的时候情况是一样的,因为是严格摆动序列,具体可以推一下。
此外,当满足构成最终是上升的摆动序列的时候,其长度一定大于等于前 i-1 个元素中最终是上升的摆动序列。即上述当 nums[i]>nums[i-1]的时候,down[i]+1 >= up[i-1],具体也可以像上述一样画图推一下。
所以最终的状态转移方程就出来了。
up[i] = up[i-1] (nums[i] <= nums[i-1])
up[i] = down[i] + 1 (nums[i] > nums[i-1])同理,下降序列也是一样的
down[i] = down[i-1] (nums[i] >= nums[i-1])
down[i] = up[i] + 1 (nums[i] < nums[i-1])
其最终结果就是 max(up[n-1],down[n-1]),代码如下:
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return n;
}
vector<int> up(n), down(n);
up[0] = down[0] = 1;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1]) {
up[i] = down[i - 1] + 1;
down[i] = down[i - 1];
} else if (nums[i] < nums[i - 1]) {
up[i] = up[i - 1];
down[i] = up[i - 1] + 1;
} else {
up[i] = up[i - 1];
down[i] = down[i - 1];
}
}
return max(up[n - 1], down[n - 1]);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# o(n)dp 再优化
由于上面的状态转移方程中只用了 up[i-1],down[i-1],就是前一个元素,因此可以省去数组,只用一个变量即可。
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return n;
}
int up = 1, down = 1;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1]) {
up = down + 1;
} else if (nums[i] < nums[i - 1]) {
down = up + 1;
}
}
return max(up, down);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 贪心
这个题还可以用贪心,关于贪心,我直接上图!
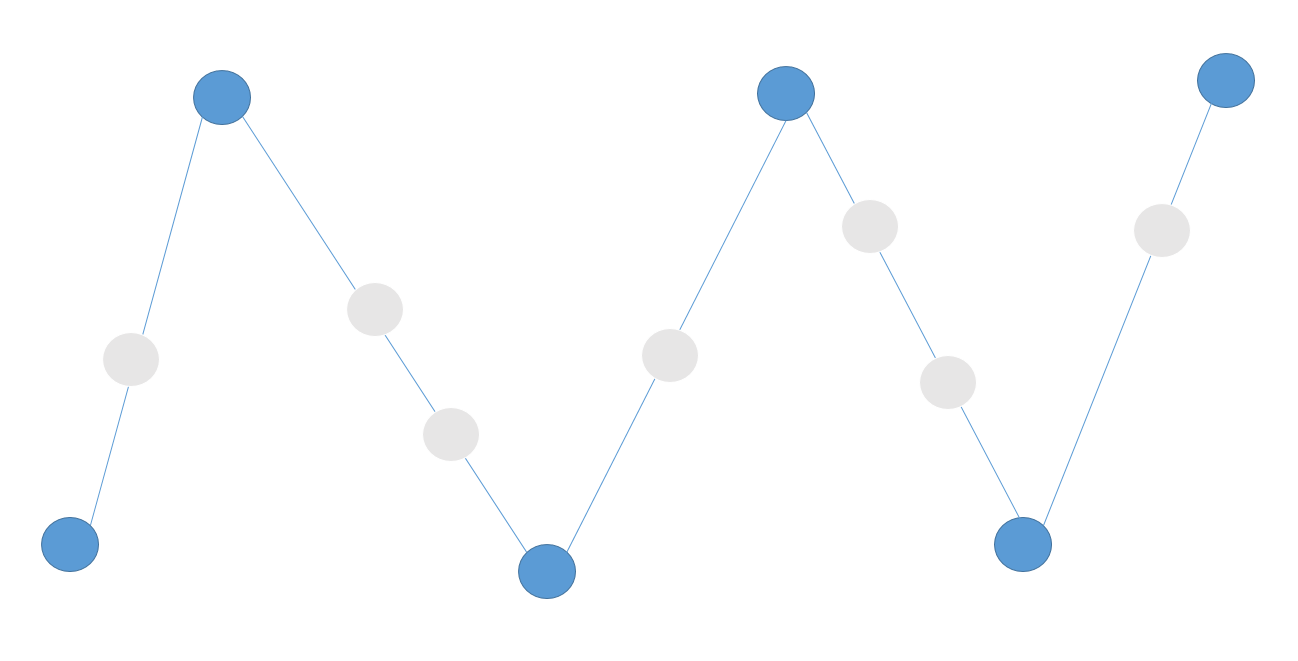
先看这个图蓝色的小球,是最初的序列,可以很直观的看出这个序列全部都可以拿去当做摆动序列,此时,如果我们在图中插入一些灰色小球,那么这时候的新序列的最大摆动子序列的长度是多少呢?
其答案还是 6,为什么呢?你可以将新插入的灰色的小球当作波峰或者波谷,你会发现其最大序列长度依然不会变化。这样的话,我们就可以每次只选择波峰或者波谷的元素就可以了,这样就可以直接统计序列长度。所谓波峰就是相邻元素都小于它,波谷就是相邻元素都大于它,但要注意两端边界。
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return n;
}
int prevdiff = nums[1] - nums[0];
int ret = prevdiff != 0 ? 2 : 1;
for (int i = 2; i < n; i++) {
int diff = nums[i] - nums[i - 1];
if ((diff > 0 && prevdiff <= 0) || (diff < 0 && prevdiff >= 0)) {
ret++;
prevdiff = diff;
}
}
return ret;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 总结
这个题不是很好想最优的解法,要一步一步迭代出来。而且其贪心算法的解法更不好想,针对于贪心,其实有很多种想法,但并不是每一种都能找出正确答案,有时候很明显这样找下去就一定是对的,但有的时候就不一定了,一定要证明一下或者大概思考一下其正确性。
